Veri Modelleme Nedir? Nasıl Yapılır?

Bu yazıda veri modellemenin nasıl yapıldığını, E-R modelleme yapısının ne olduğunu nasıl uygulandığını göstereceğim.

E-R Model Nedir?

Varlık kümelerinin arasındaki ilişkiyi göstermeye E-R diagramı denir. Varlık grubu, benzer varlıklardan oluşan bir gruptur ve bunlar aynı niteliklere sahip olabilirler.

E-R Modelinin Yapıları

E-R modelin temelde “entity”,” attribute” ve “relationship” olmak üzere üç bileşeni vardır. Şimdi sırayla bu bileşenlerin neler olduğuna bakalım.

Entity (Varlık)

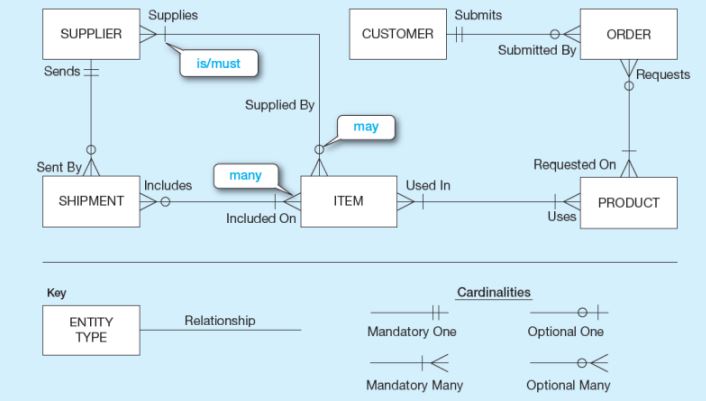
Var olan ve benzerinde ayırt edilen her şey “entity” olarak adlandırılır. Modelin en temel öğesidir, birden fazla varlık bir küme oluşturuyorsa buna “varlık kümesi” adı verilir. Model içerisinde dikdörtgen ile gösterilir. Ayrıca, bir varlık strong ve ya weak olabilir.
Örnek: öğrenci, araba, ders, kitap..

• Strong Entity: Herhangi diğer varlık türünden bağımsız mevcut olabilen varlıklar “strong” olarak adlandırılır.
Örnek: Üniversite, Araba, Ders..

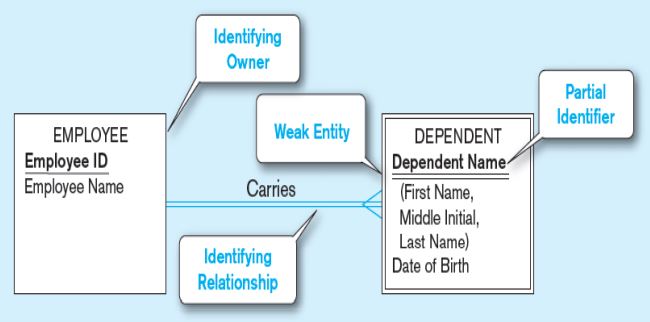
• Weak Entity: Bir varlık anahtar niteliğie sahip değilse “weak” olarak adlandılır ve weak olanlar da “iç içe kare” şeklinde gösterilirler. Weak entity, kendisini belirleyen entity ile belirleyici bir ilişki içinde olmalıdır.
Örnek: Bir fakülte üniversite olmadan var olamayacağı için fakülte zayıf bir varlıktır.

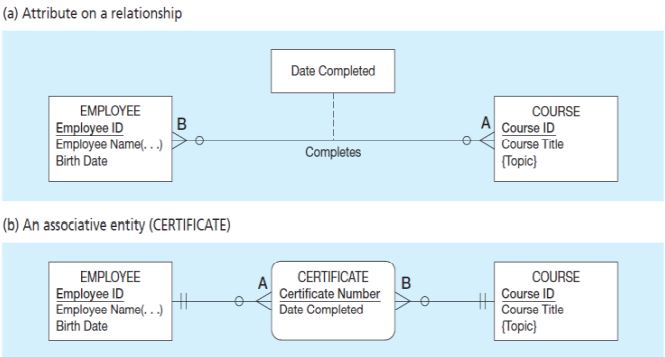
Associative Entity (İlişkilendirilmiş Varlık)

Bu varlık türü kardinalitesi many to many olan ilişkilerde kullanılır. Kare içerisinde baklava dilimi ya da oval bir biçimde bir kare şeklinde gösterilebilir. Diğer varlıklardan bağımsız anlamlı bir varlık olabilir.

Attribute (Nitelik)

Varlıkların her bir özelliği “attribute” olarak ifade edilir. Niteliğin bulunduğu varlığa düz çizgi ile bağlanır ve veritabanında her tablonun bir sütununu ifade eder. Niteliğin değeri her bir varlık için farklıysa anahtar nitelik olarak belirlenir ve şema içinde altı çizilir. Composite, multi valued ve derived attribute olarak üç alt başlığa ayrılır. Model içerisinde elips şeklinde gösterilir. Kesik çizgi ile varlıklara da bağlanabilirler.
Örnek: ad, soyad, dersKodu, dersAdi, ogrNo

• Composite Attribute: Birden fazla niteliğin birleşmesi ile oluşan niteliktir.
Örnek: Sokak, semt, apartman, daire nitelikleri birleştiğinde ev adresini oluşturur. 

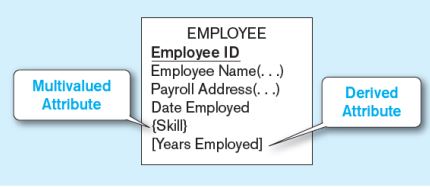
• Multi-Valued Attribute: Birden fazla değer ile eşleşebilen niteliklerdir. Bu nitelikler diagram içinde “{}” parantezi ile gösterilirler.
Örnek: Öğrenci birden fazla ders alabilir, öğretmen birden fazla ders verebilir.

• Derived Attribute:  Değerler başka bir nitelik yardımıyla üretilebilir. Bu tür nitelikler “derived” olarak adlandırılır. Başka bir nitelikten türetilen bu nitelikle ise “[]” parantezi ile gösterilirler.
Örnek: Doğum tarihi niteliği ile yaş hesaplanabilir, işe girme tarihi niteliği ile kaç yıllık çalışan olduğu hesaplanabilir. 

Relationship (İlişki)

Farklı varlık kümeleri arasındaki ilişkilere “relationship” adı verilir. Varlık kümeleri arasında çoklu ilişli olabilir ve bunlar 1-1, 1-n ve n-m ilişki olarak alt başlıklara ayrılır. İlişki kurulan varlıklara düz çizgi ile bağlanır. Diagramda baklava dilimi şeklinde gösterilir.
Örnek: Öğrenci ve dersler arasındaki ders alma ilişkisi

Identifiers (Keys) 

Tanımlayıcı (Anahtar) – bir varlık tipinin bireysel örneklerini benzersiz şekilde tanımlayan bir özelliktir. Candidate (aday) tanımlayıcı – tanımlayıcı olabilecek bir öznitelik; tanımlayıcı olma gereksinimlerini karşılar. Tanımlayıcılar,

• Değerleri değiştirilemez,
• Null değer alamazlar.
• Akıllı tanımlayıcı olmamalıdır. Örneğin, konum içeren ya da değişebilen bir insan.
• Composite (Birden fazla değerin birleşmesiyle oluşan) ve Simple olabilirler.
• Eğer bir key birden fazla varlığın değerinin birleşiminden oluşuyorsa buna “composite identifier” adı verilir. 
• Eğer bir weak entity identifier’a sahip ise buna “partial identifier” adı verilir. Partial identifier diyagramda altı çift çizgi ile belirtilir.

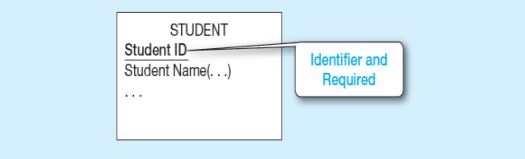
Simple Identifier

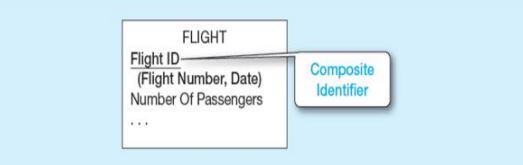
Composite Identifier

İlişkileri Modelleme (Modelling Relationships)

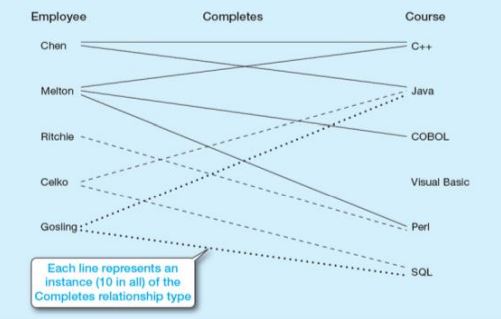
İlişki türü, varlık türleri arasındaki çizgiler olarak modellenir. İlişki örneği, belirli varlık örneği arasındadır. İlişkiler niteliklere sahip olabilir, bu nitelikler ilişkideki varlıklar arasındaki ilişkiye dair özellikleri tanımlar.

İki varlık arasında birden fazla ilişki türü olabilir (multiple relationships)

İlişkilerin Derecesi

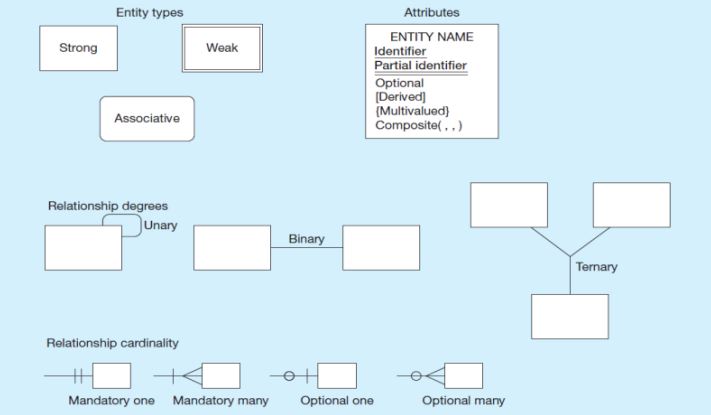
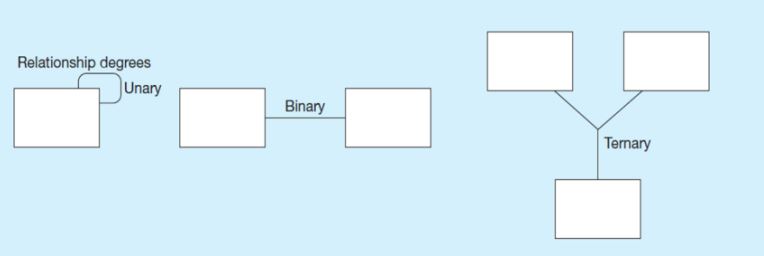
Bir ilişkinin derecesi, ona katılan varlık türlerinin sayısıdır. Unary, Binary ve Ternary İlişki olmak üzere 3 alt başlığa ayrılır.

Unary Relationship: Birbiriyle ilişkili aynı varlık tipindeki varlıklar.

Binary Relationship: Bir türün varlıkları diğerinin varlıklarıyla ilişkilidir.

Ternary Relationship: Aynı ilişkide yer alan üç farklı türden varlıklar.

İlişkilerin Kardinalitesi

One to One Relationship: Her bir varlık sadece bir tane varlıkla ilişki kurduğu relationship türüdür.

One to Many Relationship: İlişkinin bir tarafındaki bir varlığın birçok ilgili varlığı olabilir, ancak diğer taraftaki bir varlığın maksimum bir ilgili varlığı olacaktır.

Many to Many Relationship: İlişkinin her iki tarafındaki varlıklar, diğer tarafta birçok ilişkili varlığa sahip olabilir.

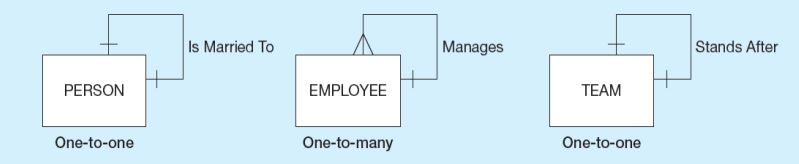
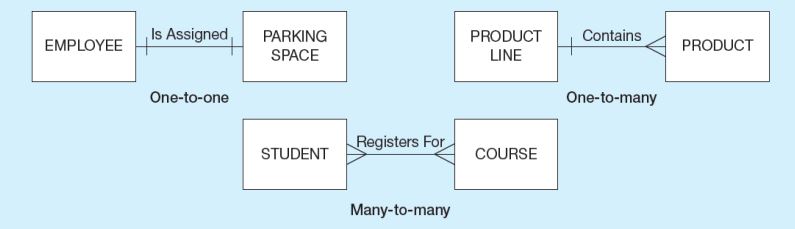
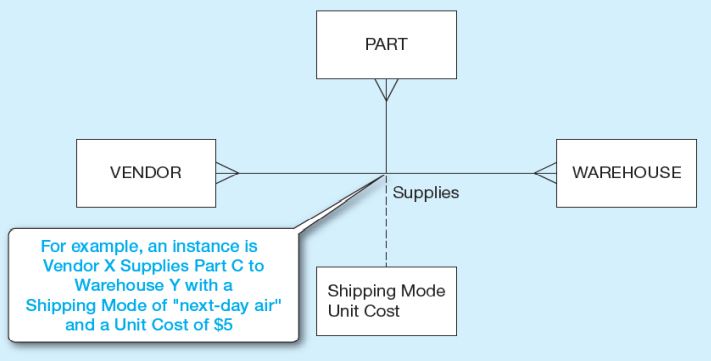
Eğer kardinalite 0 ise, ilgili varlığın değeri opsiyoneldir. Eğer kardinalite bir veya birden fazla ise varlığın değeri zorunludur. Kardinalite herhangi bir sayı ile de gösterilebilir, bu sayı maksimum sayıyı ifade eder. Dıştaki çizgiler maksimumu, içteki çizgiler minimumu ifade eder.

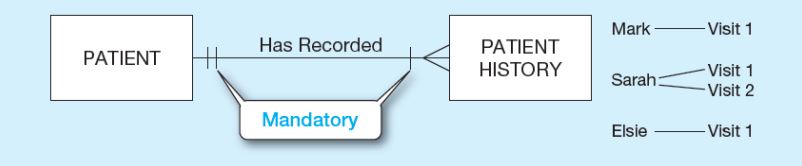
Yukarıdaki örnekte hasta ve hasta kaydıyla ilgili bir zorunluluk söz konusudur. Çünkü hasta olmadan hasta kaydı olamaz. Ayrıca, bir hastanın birden fazla hasta kaydı olabilir mi? Evet, olabilir. Bunu “Patient History”‘nin solundaki (dıştaki) çizgi ile many olduğunu belirtiyoruz. Ek olarak, yine dikkat edilirse, bir hasta kaydının birden fazla hastası olabilir mi? Hayır, olamaz. Çünkü hastanın en soldaki çizgisi 1’dir.

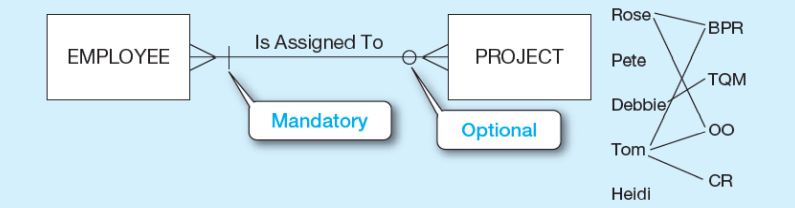
Bu örnekte de dikkat edilirse, her bir çalışan bir projede çalışmak zorunda değil. Ancak, bir proje varsa projenin çalışanı olmak zorunda. Ayrıca, çalışanda bulunan ilk çizgiden bir projede sonsuz sayıda çalışan olduğunu söyleriz. Çalışana bağlı olan ikinci çizgi ise bir projede en az bir çalışan olması gerektiğini belirtir. Şimdi projeye gelelim. Projedeki en sağ çizgi ise bir çalışanın birden fazla projede çalışabildiğini gösterir. Projedeki çizi 0 ise bir çalışanın hiçbir projede çalışmayabileceğini gösterir.

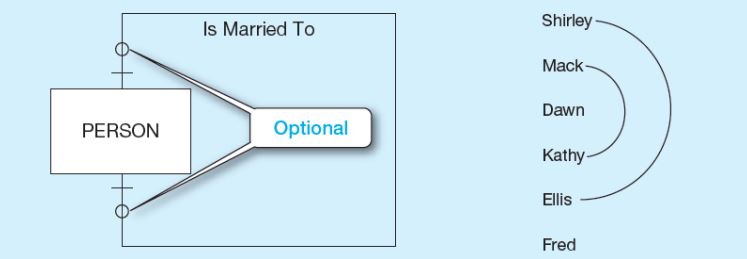
Bu örnekte de, bir kişi öncelikle sadece bir kişi ile evli olabilir. Ancak, kişi evli de olmayabilir. Diyagramda kişinin tek kişi evlenmesi çizgi ile kişinin evli ya da evli olmamasının opsiyonel durumu 0 ile gösterilmiştir.

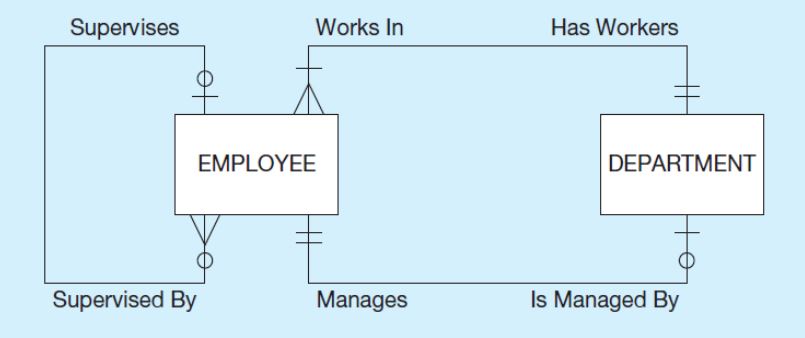
Yukarıdaki diyagramı yorumlayalım.

• Andrei adında bir çalışanımız olsun. Andrei deparment üzerindeki ilk çizgiden dolayı en fazla bir departmanda çalışabilir.
• Deparment üzerindeki ikinci çizgi ise en az bir departmanda çalışan olması gerektiğini söyler. Örneğin, Ahmet adında bir çalışan olsun, bu çalışan en az bir departmanda çalışmak zorundadır.
• Ahmet adında bir çalışan olsun, Ahmet birden fazla departmanı yönetebilir mi? Hayır yönetemez. Çünkü department altındaki ilk çizgi maksimum sayıyı ifade eder. O da birdir. 
• Ahmet hiçbir departmanı yönetmiyor olabilir mi? Evet, yönetmeyebilir. Bunu da departmentin en altındaki 0’dan anlıyoruz.
• Hakan adında bir çalışan olsun ve Hakan üzerinde 1000 çalışan bağlı olsun. Bu mümkün müdür? Evet, mümkündür. Employee’nin sol tarafında altındaki ilk çizgi bu durumu ifade eder.
• Ferda adında bir çalışanımız olsun. Bu Ferda aynı zamanda hem Hakan’a hemde Ahmet’e raporlama yapabilir mi? Hayır yapamaz. Çünkü Employee’nin sol tarafında üstündeki ilk çizgi bu durumu ifade eder.
• Ferda, hiçkimseye raporlama yapmıyor. Bu mümkün müdür? Evet, mümkündür. Employee’nin sol tarafında üstündeki ikinci çizgi olan 0 ise bu durumu ifade eder.
• Bir departmanda 500 tane çalışan olabilir mi? Evet, olabilir. Bunu Employee’nin sağ tarafında üstündeki ilk çizgiden anlıyoruz. 
• Bir departmanda hiç çalışan olmayabilir mi? Hayır, olamaz. Bunu da Employee’nin sağ tarafında üstündeki ikinci çizgiden anlıyoruz. Buradaki tek çizgi en az minimum bir çalışan olması gerektiğini ifade eder.
• Bir departmanı birden fazla kişi yönetebilir mi? Hayır, yönetemez. Bunu departmentin altındaki ilk çizgiden anlıyoruz. Çünkü ilk çizgi maksimumu ifade etmekteydi.
• Bir departmanı hiçkimse yönetmeyebilir mi? Hayır, her bir departmanın en az bir yöneticisi olmak zorunda. Bunu da departmentin en altındaki çizgiden anlıyoruz. Bu çizgi de minimumu ifade etmekteydi.

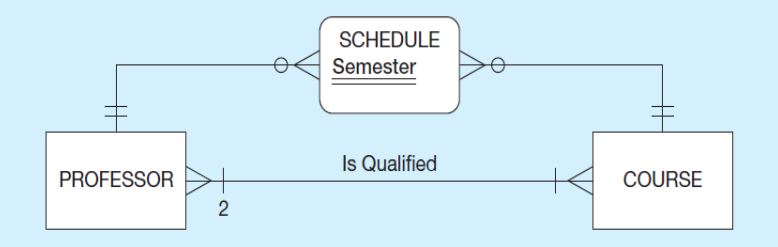
Yukarıdaki diyagramda öncelikle “Profesor” ve “Course” birer entity. “Schedule” ise oval kare ve many to many ile birden fazla varlığa bağlandığı için bir associative entity’dir. Dikkat edilirse, Semester’ın altında iki tane çizgi mevcuttur. Bu Semester’ın partial identifier olduğunu gösterir. Yukarıdaki diagrama göre;

• Bir profesör birden fazla ders verebilir.
• Bir ders birden fazla hoca tarafından alınabilir.
• Bir dersin verilebilmesi için en az 2 tane profesör gereklidir.

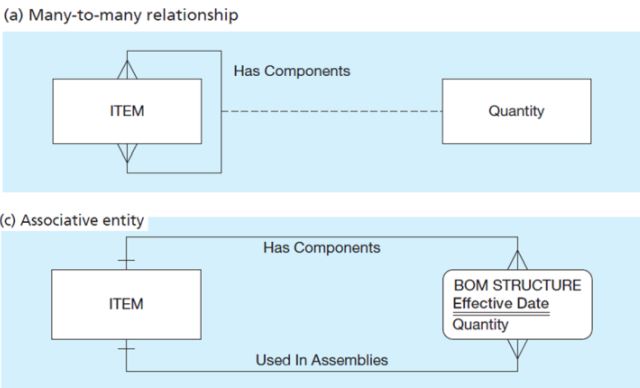
Yukarıdaki diyagramlarda many to many ilişki associative entity şekline dönüştürülmüştür. Veritabanı modellemesi yapılırken mümkün olduğunca ternary relationship türünden kaçınılması gerekir. Mümkün olduğunca binary relationship yapısı tercih edilmelidir.

Enhanced E-R Model

Geliştirilmiş E-R Model de ekstra olarak supertype ve subtype kavramlarını göstereceğim. Peki nedir bu supertype ve subtype kavramları? Bir veya daha fazla alt türle ilişkisi olan genel bir varlık türü “supertype” olarak adlandırılır. Diğer alt gruplardan farklı niteliklere sahip bir varlık tipindeki varlıkların bir alt grubuna ise “subtype” adı verilir.

Attribute Inheritance

• Alt tür varlıkları, süper türün tüm özniteliklerinin ve ilişkilerinin değerlerini devralır.
• Bir alt türün örneği, aynı zamanda bir üst türün örneğidir.

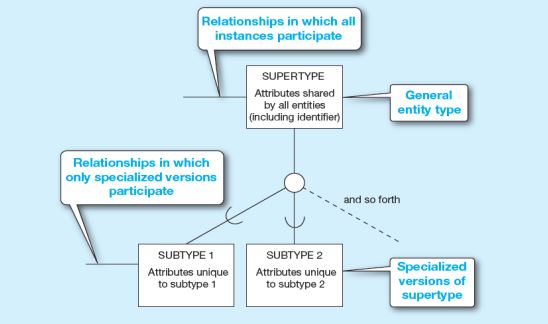
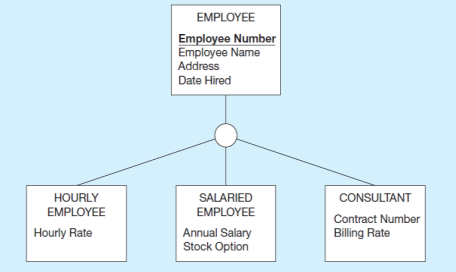
Yukarıdaki diyagramda, tüm çalışan alt tiplerinde çalışan numarası, adı, adresi ve işe alınma tarihi mevcuttur. Her çalışan alt türünün de kendi nitelikleri olacaktır.

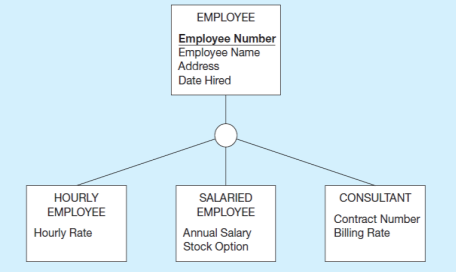
Supertype seviyesindeki ilişkiler, tüm subtypların ilişkiye katılacağını gösterir. Bir alt türün örnekleri, o alt türe özgü bir ilişkiye katılabilir. Bu durumda ilişki alt tip düzeyinde gösterilir.

Generalization ve Specialization Kavramları

Generalization 

Bir dizi daha uzmanlaşmış varlık türünden daha genel bir varlık türünü tanımlama sürecidir. (BOTTOM-UP)

Specialization

Süper tipin bir veya daha fazla alt tipini tanımlama ve süper tip/alt tip ilişkileri oluşturma sürecidir. (TOP-DOWN)

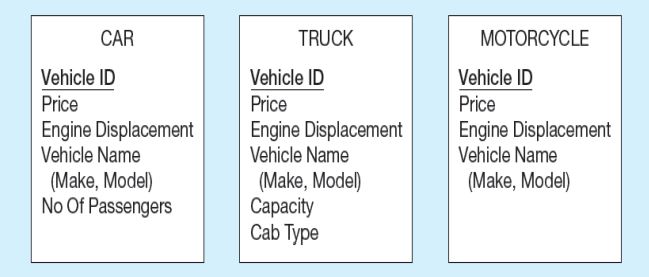
Yukarıdaki diyagramda CAR, TRUCK ve MOTORCYCLE entity olmak üzere, bütün entityler ortak bir price, Engine Displacement, Vehicle Name gibi ortak niteliklere sahipler.

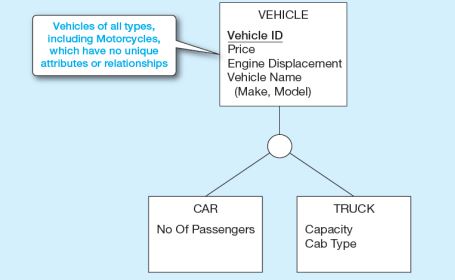
Paylaşılan nitelikleri bir süper tipe koyarız. Ek olarak, benzersiz niteliklere sahip olmadığı için motosiklet için alt tip yoktur.

Yukarıdaki diyagramda parça imalatı yapmak amacıyla oluşturulmuş “PART” adında bir entity mevcut. Bu PART entity için specialization (genelden özele inme) işlemini gerçekleştirelim.

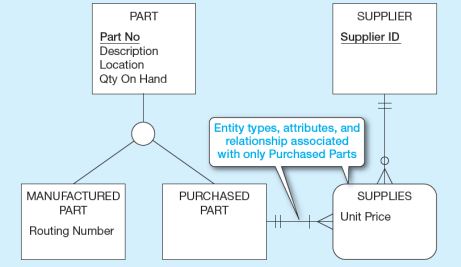
Burada SUPLIER (Tedarikçi) oluşturulup, PART entity, MANUFACTURED PART ve PURCHASED PART olarak özelleştirildi.

Supertype ve Subtype İlişkilerde Kısıtlamalar

Completeness ve Disjointness kısıtlamalarını ele alacağız.

Completeness Constraints: Bu durumda kısıtlamaları “Total Specialization Rule” ve “Partial Specialization Rule” olarak ikiye ayırırız. Total specialization, çift çizgi ile gösterilir ve ilgili entity’den aşağıya doğru inilmesi gerektiğinin zorunlu olduğunu belirtir. Partial specialization ise tek çizgi ile gösterilir ve ilgili entity’de kalınabilir ya da aşağıya da inilebilir olduğunu gösterir.

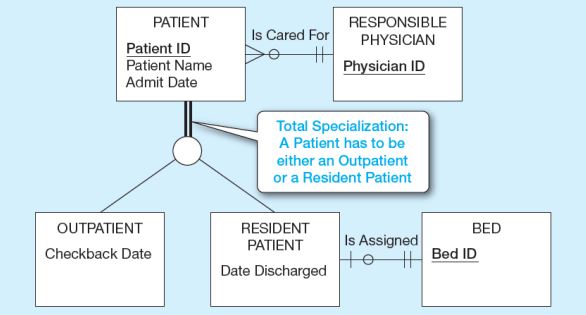
Bir hasta olsun, bu hasta ya yataklı hastadır ya da ayakta hastadır. Dolayısıyla burada total specialization uygularız. Hastadan aşağıya inen çizgi çift çizgi ile gösterilir. 

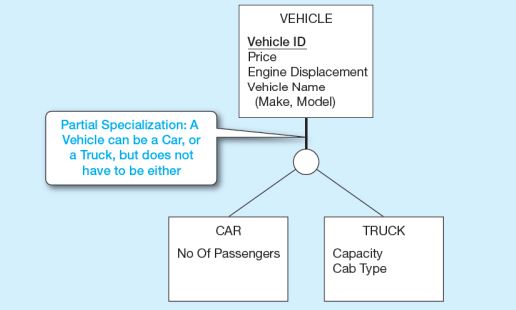
Bir araç olsun, bu araç “CAR” ve “TRUCK” olabildiği gibi bunlar dışında da başka bir şey olabilir. Örneğin, motorsiklet olabilir. Dolayısıyla, ilgili “VEHICLE” varlığından aşağıya inmek zorunda değiliz. Dolayısıyla, burada tek çizgi kullanılır.

Disjointness Constraints: Şuana kadar ilgili varlıkta kalmaya ya da aşağısına inmeyi konuştuk ancak, ilgili varlıktan aşağı inerken ya da yukarda kalırken bunların kombinasyonlarından bahsetmedik. İşte disjoitness bu durumla ilgilenir. Bu durumu da kendi içerisinde “Disjoint Rule” ve “Overleap Rule” olarak ikiye ayırırız. Disjoitness, kombinasyona müsade etmez. Overleap ise müsade eder.

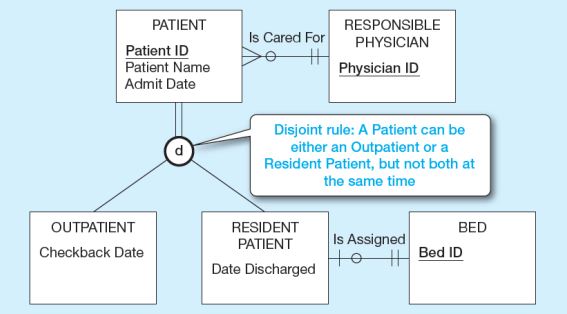
Burada, çift çizgiyi yukarıda konuşmuştuk. Şimdi “d” harfi disjointi ifade eder. Dolayısıyla, burada bir hasta ya ayakta olmalıdır ya da yatan hasta olmalıdır. Disjointten dolayı, bir hasta hem yatan hem de ayakta bir hasta olamaz. Bunların kombinasyonuna izin vermez.

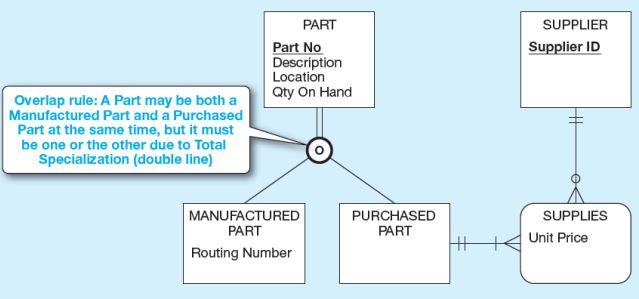
Bu örneğimizde ise parça üretilen bir parça ya da imal edilen bir parça olabilir. Çift çizgiden, parçadan aşağıya inmemiz gerektiğini anlıyoruz. “O” ise bunun overleap olduğunu bir parçanın hem imal edilen hem de üretilen bir parça olabileceğini ifade eder. Dolayısıyla bunların bütün kombinasyonlarına izin verir.