Doğru veya yanlış mutlak olan ifadelere “Önerme” denir. Önermeler genel olarak harflerle (p, q, r, s.. vb.) gösterilirler. Önermeler, emir, ünlem ve soru cümleleri ile karıştırılmamalıdır. Peki bu önermeler nerelerde kullanılır? Önermeler birçok yerde karşımıza çıkabilir örnek vermek gerekirse; bilgisayarlar üzerinde Input/Output  birimlerinde, bilgisayarların depolama birimlerinde (Binary Logic) kullanılır. Önermelere geçmeden önce, Ünlem, soru ve emir cümlelerini öne[the_ad_placement id=”adsense-in-feed”]rmeler ile karıştırmamak gerekir. Örneğin;

“Türkiye’nin yüz ölçümü 783,562 km²’dir.”

Bu cümle bir önermedir çünkü doğru veya yanlış bir kesin hüküm bildirmektedir.

“Bugün ne yapacaksın?”

Bu cümle ise bir soru cümlesidir, soru cümleleri kesinlikle bir önerme değildir, kesin bir hüküm içermez.

“Bana su getir!”

Bu cümle ise bir emir cümlesidir, emir cümleleri önermeler içine dahil edilmez.

“Ne kadar güzel!”

Bu cümle de bir ünlem cümlesidir, doğrulu veya yanlışlığı bilinemez, kesin bir hüküm içermediğinden önermeler içine dahil edilemez.

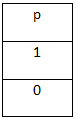
Bir önermenin değeri

Önermeler doğruluk değerlerinden oluşurlar, bir önerme iki kesinlikten birini içerebilir ya kesinlikle, doğrudur ya kesinlikle yanlıştır. Doğru olan önermeler “1” değeri ile veya “(D)”, yanlış olan önermeler ise “0” ile veya “(Y)” ile ifade edilir.

İki önermenin değeri doğru yani “1” ise, bu önermeler birbirine denktir, denk olan bu önermeler “≡” işareti ile gösterilir. Örneğin, p önermesi “Türkiye’nin başkenti Ankara’dır.”, q önermesi ise “Dünya geoit bir şekle sahiptir.” iki önerme de doğrudur, iki önermenin değeri de “1”dir.

p: Türkiye’nin başkenti Ankara’dır.

q: Dünya geoit bir şekle sahiptir.

dolayısıyla bu önermeler birbirine denktir. Yani p ≡ q olarak gösterilebilir.

Bir önermenin doğrulunun ya da yanlışlığının değiştirilmesine “Önermenin Olumsuzu/Değili” denir ve “tırnak (‘)” işareti ile gösterilir. Örneğin p: 100+2 = 102 olsun önermenin değeri 1’dir. Ancak bu önermenin değili p’ olarak gösterilir ve değili 0’dır.

Yani, p ≡ 1 ise, p’ ≡ 0 olur.

Ayrıca, n tane önermenin 2n  tane doğruluk değeri vardır.

Birden fazla önermenin çeşitli bağlaçlarla birbirlerine bağlanmasıyla oluşan önermelere “Bileşik Önermeler” denir. Bu bağlaçları sırasıyla görelim;

1) Ve Bağlacı: p ve q iki önerme olsun, bu iki önermenin doğruluk değerinin 1 olduğu durumda 1, bir tanesinin veya her ikisinin de yanlış olması durumunda 0 döndüren bağlaçtır. “∧” ile gösterilir. Ve bağlacının doğruluk tablosu aşağıdaki gibidir..

Mantık ve Tablosu

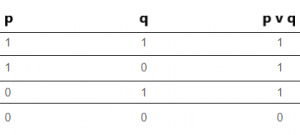
2) Veya Bağlacı: p ve q iki önerme olsun, bu iki önermenin doğruluk değerinin yalnız bir tanesinin 1 olması, 1 değeri döndürmesi için yeterlidir. “v” ile gösterilir. Veya bağlacının doğruluk tablosu aşağıdadır..

Ve / Veya Bağlacındaki Özellikler:

a) Tek Kuvvet Özelliği: Önermelerinin birbirlerine göre ve/veya bağlacındaki durumları birbirlerine denktir.
p v p ≡ p
p ∧ p ≡ p

b) Değişme Özelliği: Farklı iki önermenin ve/veya bağlacındaki konumları yer değiştirebilir.
p v q ≡ q v p
p ∧ q ≡ q ∧ p

c) Birleşme Özelliği: Farklı önermelerin parantez içinde veya dışında birleşme durumudur.
p v (r v q) ≡ (r v p) v q
p ∧ (r ∧ q) ≡ (r ∧ p) ∧ q

d) Dağılma Özelliği: Ve/Veya bağlaçlı bileşik önermelerinin birbirlerine dağılma durumudur.
p ∧ (q v r) ≡ (p ∧ q) v (p ∧ r)
p v (q ∧ r) ≡ (p v q) ∧ (p v r)

Ayrıca,
p v 0 ≡ p,    p v 1 ≡ 1,    p v p’ ≡ 1
p ∧ 0 ≡ 0,    p ∧ 1 ≡ p,   p ∧ p’ ≡ 0

Bileşik Önermelerde Olumsuzluk (Değili) Kavramı:
De Morgan Kuralı: Bileşik önermelerinin tümleyen alma durumuna “De Morgan Kuralı” denir. Kuralı De Morgan adlı İngiliz bir matematikçi bulduğundan “De Morgan Kuralı” adı verilmiştir. Kuralara göre değerler aşağıdaki tabloda gösterilmiştir.

De Morgan Kuralı Tablosu

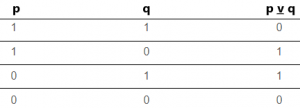
3) Ya da Bağlacı: p ve q, birer önerme olsun bu önermelerden yalnızca birinin 1, olduğu durumlarda 1 değerini verir. Aynı anda iki doğruluk kabul edilemez. Örneğin, bugün yapmak için önünüzde iki seçenek var; biri telefonunuzla oynamak, diğeri ders çalışmak. Siz bu seçenekten birini seçmek zorundasınız ya telefonla oynamayı seçersiniz ya da ders çalışmayı seçersiniz; her iki eylem aynı anda yapılamaz. Ya da bağlacı “v” işareti ile gösterilir. Ya da tablosunun doğruluk değerleri aşağıdaki tablodaki gibidir.

Mantık yada Tablosu

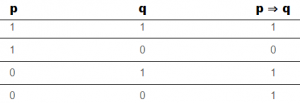
4) İse Bağlacı (Şartlı/Koşullu Önerme): p ve q birer koşullu önerme olsun, p birinci önerme, q ise ikinci önerme, p≡1, q≡0 olduğu durumda 0, diğer bütün durumlarda 1 değeri döndüren bir bağlaçtır. “⇒” işareti ile gösterilir. p ⇒ q önermesi, p’ v q önermesine örnektir.  Doğruluk tablosu aşağıdadır..

p ⇒ q ≡ p’ v q

Ayrıca, p ⇒ q şartlı önermesinde;
p’ye “hipotez”, q’ya ise “hüküm” denir, eğer önermenin doğruluk değeri 1 ise, bu şartlı önermeye “gerektirme” adı verilir. Önermede q, p için gerek koşul, p önermesine ise, q için gerek koşul denir.
p ⇒ p ≡ 1
p ⇒ p’ ≡ p’
p’ ⇒ p ≡ p
1 ⇒ p ≡ p
p ⇒ 1 ≡ 1
0 ⇒ p ≡ 1
p ⇒ 0 ≡ p’

Koşullu Önermenin Karşıtı, Tersi ve Karşıt Tersi:
p ⇒ q önermesinin,
Karşıtı; q ⇒ p,
Tersi; p’ ⇒ q’
Karşıt Tersi; q’ ⇒ p’

5) Ancak ve Ancak Bağlacı (İki Yönlü Şartlı Önerme): p ve q birer önerme olmak üzere, p ve q’nun değerleri aynı (ikisi 1 veya ikisi 0) iken 1 değerini döndüren iki yönlü şartlı önermedir. “⇔” işareti ile gösterilir.

p ⇔ q ≡ (p ⇒ q) ∧ (q ⇒ p)

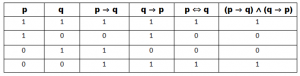
Ancak ve Ancak Bağlacı

Eğer p ⇔ q önermesinin doğruluk değeri 1 ise bu önermeye “çift gerektirme” adı verilir.
p ⇔ 1 ≡ p
p ⇔ 0 ≡ p’
p ⇔ p ≡ 1
p ⇔ p’ ≡ 0

Bir bileşik önermede, önermeyi oluşturan önermelerin tüm doğruluk değerleri için daima 1 dönüyorsa bu önermeye “Totoloji”, eğer tüm doğruluk değeri için 0 dönüyorsa “Çelişki” denir.
p v p’ ≡ 1 (Totoloji)
p ∧ p’ ≡ 0 (Çelişki)
p ⇔ p’ ≡ 0 (Çelişki)

Önüne gelen elemanların niceliğini bildiren “Her (∀)” ve “Bazı (∃)” sözcüklerine “Niceleyici” denir. Bazı niceleyicisinin tersi her, her niceleyecisinin tersi ise bazıdır.

“∃x, p(x)” önermesi “en az bir x için p(x)” diye okunur.
“∀x, p(x)” önermesi “her x için p(x) diye okunur.

“∃x, p(x)” önermesinin doğrulunu kanıtlamak için, p(x)’i doğru gösteren bir örnekleme kafidir.
“∀x, p(x)” önermesinin yanlışlığını göstermek için, p(x)i yanlış gösteren bir örnekleme kafidir.

Son olarak,
Bir kavramın niteliklerinin hepsini belirtmeye “tanım”,
Doğruluğu ispatsız olarak kabul edilen önermelere “Aksiyom”,
Doğruluğu ispatlanması gereken önermelere “Teorem” denir. Teoremin ispatlanacak kısmına “hüküm”, verilen kısmına ise “hipotez” adı verilir.

Görüntüleme Sayısı: 134.362