Kümeler – Konu Anlatımı

Herhangi tür objeleri (sayılar, harfler, kelimeler, cümleler) barındıran; bu barındırdığı objelerin kesin hükmünde olması, herhangi bir belirsizlik olmaması şartıyla tanımlı olan grup ya da topluluğa “Küme” denir.

Kümelere örnek verecek olursak; pozitif çift sayılar, asal sayılar, tek sayılar, 20’den küçük doğal sayılar birer küme belirtir.

• Ayrıca, kümeler isimlendirilirken büyük harfler atanır.
• A bir küme olsun, bu kümenin eleman sayısı “s(A)” şeklinde gösterilir.
• Kümenin oluştuğu her bir objeye “eleman” adı verilir ve “∈” ile gösterilir.
• Bir kümeye bir eleman sadece bir kez yazılır. Örneğin bir kümede 2 rakamı aynı anda bulunmaz.

Küme Çeşitleri:
1) Boş Küme: Hiçbir elemanı olmayan kümelerdir. “{ }” ya da  “ø” sembolleriyle gösterilir. Ayrıca, {ø} veya {0} kümeleri birer boş küme değildir. Çünkü eğer dikkat edilirse burada küme içerisinde bir obje bulunmaktadır.

2) Denk Küme: Eleman sayısı birbirine eşit olan kümelerdir. Birbirine iki denk küme “≡” işaretiyle gösterilir.
A = {101, 102, 103, 104}
B = {1, 2, 3, 4}
Eleman sayıları birbirine eşit olduğundan yani, s(A) = 4,  s(B) = 4 olduğu için, bu kümeler birbirine denktir. (A ≡ B)

3) Eşit küme: Elemanlarıyla birebir örtüşen kümelere eşit kümeler denir. Eşit kümelerin, eleman sayısı ve elemanları birbirine eşittir.
A = {2, 4, 6, 8}
B = {2, 4, 6, 8}
Burada elemanlar ve eleman sayıları birbirine eşit olduğundan bu kümeler birbirine eşittir. (A=B)

4) Ayrık Küme: Ortak elemanı bulunmayan kümelerdir.
A = {101, 102, 103, 104}
B = {1, 2, 3, 4}
Kümeleri ortak eleman bulundurmadıklarından ayrık kümelerdir.

5) Sonlu Küme: Elemanları sayılabilen kümeledir.
A = {x | 1 < x < 9, x ∈ Z+}
Burada 1 ile 9 aralığında 2,3,4,5,6,7 ve 8 pozitif tamsayılar vardır.

6) Sonsuz Küme: Elemanları sayılamayan kümelerdir.
A = {x | 1 < x < 9, x ∈ R}
Burada 1 ile 9 arasında sonsuz tane reel sayılar vardır.

7) Alt Küme: A ve B birer küme olsun, B kümesinin her elemanı A kümesinin de elemanı ise, B’ye A’nın alt kümesidir denir ve B⊂A (B alt kümesidir A’nın) ya da A⊃B (A kapsar B’yi, A, B’nin üst kümesidir) şeklinde gösterilebilir.

– Her küme kendisinin bir alt kümesidir, bu duruma “Yansıma Özelliği” denir.

– Boş küme her kümenin bir alt kümesidir, bu duruma “Etkisiz Eleman Özelliği” denir.

– A⊃B ve B⊃A ise A=B’dir. Bu duruma “Ters Simetri Özelliği” denir.

– [(A ⊂ B ∧ (B ⊂ C)] ⇒ (A ⊂ C) ‘dir (Geçişme Özelliği)

– n elemanlı bir kümenin alt kümelerinin sayısı; 2ⁿ 

– n elemanlı bir kümenin r elemanlı alt küme sayısı c(n, r)‘dir. Örneğin 5 elemanlı bir kümenin 2 elemanlı alt küme sayısı c(5,2) = 5.4 = 20

8) Öz alt Küme: Bir kümenin kendisinden farklı alt kümelerinin sayısıdır. n elemanlı bir kümenin öz alt küme sayısı; 2ⁿ – 1

9) Evrensel Küme: Bütün kümeleri kapsayan küme “Evrensel Küme” olarak adlandırılır. “E” ile gösterilir. Ayrıca, tüm kümeler evrensel kümenin alt kümesidir; yani evrensel küme tüm alt kümeleri kapsar.

10) Kuvvet Kümesi: Bir kümenin alt kümelerinin oluşturduğu kümedir. A bir küme olmak üzere, bu kümenin kuvvet kümesi “P(A)” ile gösterilir.
s(P(A)) = 2ⁿ 

Kümelerin Gösterim Şekilleri:
1) Liste Yöntemi: Kümedeki elemanların { } parantezinin içinde gösterimidir.
Örnek: A bir küme ve elemanları “7,8,9” olsun;  A = {7, 8 ,9}’dur.

2) Ven Şeması: Küme elemanları bir daire veya elips içinde her eleman bir nokta ile birleştirilip, noktanın yanına elemanlar yazılarak gösterilir. Örneğin A bir küme ve elemanları “7, 8, 9” olsun;

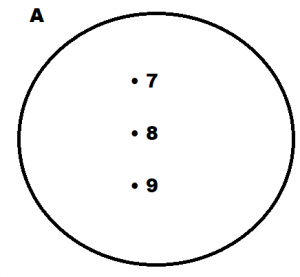
3) Ortak Özellik: Kümenin elemanlarını somut bir şekilde ya sözel veya matematiksel ifadelerle tanımlama biçimidir. Örneğin A bir küme olsun;
A = {x | (x’in özelliği),
A = {x | x>25 ∧ x<85, x ∈ N}  burada x’in 25’ten büyük ve 85’ten küçük doğal sayılar olduğu ifade edilir.

Kümelerde İşlemler:
1) Kümelerde Kesişim: İki kümede bulunan ortak elemanlar “Kesişim” ile ifade edilir ve “∩” sembolü ile gösterilir.

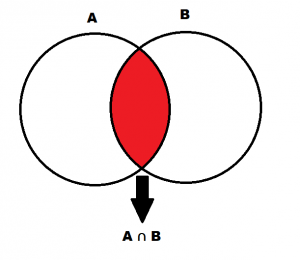
• İki ayrık (ortak elemanı olmayan)  kümenin kesişimi boş kümedir. Bu önermenin tersi de doğrudur.
• Herhangi iki kümenin kesişimi kümelerden birini veriyorsa bu veren küme diğerinin alt kümesidir. (Küçük olan küme kesişimde kesinlikle alt küme olur, büyük olan küme tarafından kapsanır.) [(A ∩ B) ≠ ø  ve (A ∩ B) = A ise; (A ⊂ B)]

A ∩ A = A (Tek Kuvvet)
A ∩ ø = ø (Yutan Eleman ø)
A ∩ B = B ∩ A (Değişme Özelliği)
(A ∩ B) ∩ C = A ∩ (B ∩ C) (Birleşme Özelliği)

2) Kümelerde Birleşim: İki veya daha fazla kümenin elemanlarını birleştirme işlemidir ve  “∪”  sembolü ile gösterilir.

• A ve B birer küme, bu kümelerin eleman sayıları toplamı; s(A ∪ B) – s(A ∩ B)‘dir. Eğer kümelerin eleman toplamları eşit ise; s(A ∪ B) = s(A) + s(B) birer ayrık kümedir.
• Herhangi iki kümenin birleşimi kümelerden birini veriyorsa; verilen küme, diğerini kapsar. [( A ∪ B) = A  ise (A  ⊃ B)’dir.]
• Eğer kümelerin birleşimi boş kümeyi veriyorsa, kümeler boş kümedir.

A ∪ A = A (Tek Kuvvet)
A ∪ ø = A (Etkisiz Eleman ø)
A ∪ B = B ∪ A (Değişme Özelliği)
(A ∪ B) ∪ C = A ∩ (B ∩ C) (Birleşme Özelliği)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ ( A ∪ C)

3) Kümelerde Fark İşlemi: A ve B birer küme, A fark B;  A’da olup B’de olmayan elemanları temsil eder. A fark B “A / B” veya “A – B” şeklinde gösterilebilir.

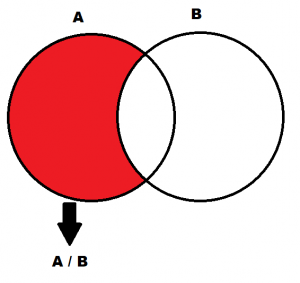
• A ve B boş kümeden farklı iki küme olsun; eğer A / B ‘de eleman olup, B / A ‘da hiç eleman yoksa B kümesi, A kümesinin alt kümesidir veya A Kümesi, B kümesini kapsar diyebiliriz.

A / A = ø
A / ø = A
ø / A = ø
A / B ≠ B / A
(A / B) ∪ B = A ∪ B
A / (B ∩ C) = (A / B) ∪ (A / C)
A / (B ∪ C) = (A / B) ∩ (A / C)

4) Kümelerde Tümleyen İşlemi: Bir kümenin dışında kalan diğer kümelerdeki elemanların oluşturduğu kümeye “Bu kümenin tümleyeni” denir ve “(‘)” (Apostrof) işareti ile gösterilir.

• Bir kümenin tümleyeninin tümleyeni kendisidir. [(C’)’ = C]
• A ve B birer küme, A kümesi, B kümesinin alt kümesi ise, A’nın tümleyeni de B’nin tümleyeninin alt kümesidir. Önermenin tersi de aynı şekilde geçerlidir.

5) De Morgan Kuralı: Küme üzerinde birleşim ve kesişim işlemlerinde tümleyen alınma durumuna “De Morgan Kuralı” adı verilir. Kuralara göre, kesişim birleşime, birleşim kesişime dönüşür.
(A ∩ B)’ = A’ ∪ B’
(A ∪ B)’ = A’ ∩ B’