Bağıntılar ve Kartezyen Çarpım Nedir?
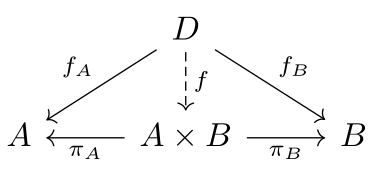
İki objenin sıralı bir şekilde oluşturulup tek bir nesne olarak yazılmasına “Sıralı İkili” denir. x, sıralı ikilinin birinci nesnesi; y, ikinci nesnesi olsun. (x, y) sıralı ikilisi;
(x, y) = (z, c) ise x = z, y = c’dir.
Kartezyen Çarpım:
Herhangi iki küme tanımlansın. Sıralı ikilinin birinci bileşeni bu kümenin birinden, ikinci bileşeni diğer kümeden olmak üzere; oluşturulan sıralı ikiliye “Kartezyen Çarpım” denir. A ve B birer küme ve A ve B’den oluşturulan kartezyen çarpım “A x B” şeklinde gösterilir.
A x B = {(a, b)} ise (a ∈ A) ve (b ∈ B)’dir.
A x Ø = Ø x A = Ø (Yutan Eleman)
A x (B x C) = (A x B) x C (Birleşme)
A x (B ∪ C) = (A x B) ∪ (A x C) (Dağılma)
A x (B ∩ C) = (A x B) ∩ (A x C) (Dağılma)
s(A) = x, s(B) = y olmak üzere, s(A x B) = x.y’dir.
Bağıntı:
A ve B birer küme olsun, A x B kartezyen çarpımının bütün alt kümesine A’dan B’ye bağıntı denir. “β (Beta)” işareti ile gösterilir.
s(A) = x, s(B) = y olsun. A’dan B’ye 2xy tane bağıntı tanımlanabilir.
Örnek: A = {8, 7} B = {9, 4, 3} olsun. Burada A’dan B’ye; 23*2 = 26 = 64 tane bağıntı tanımlanabilir.
s(A) = m ve s(B) = n olsun. A dan B ye tanımlanabilen r elemanlı (r ≤ m . n) bağıntı sayısı;
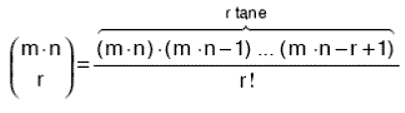
Bağıntının tersi tanımlanan bağıntıdaki elemanların yerleri değiştirilerek alınır. β ⊂ A x B olsun, β = {(a, b)} ve (a ∈ A) ve (b ∈ B) bağıntısının tersi β-1 ⊂ B x A dır. β-1 = {(b, a)}‘dır.
Örnek: A = {1, 3}, B = {7, 9} olsun, A x B = β = {(1, 7), (1, 9), (3, 7), (3, 9)},
Bu durumda, β-1 = {(7, 1), (9, 1), (7, 3), (9, 3)}’dür.
Yansıma Özelliği: A bir küme, ve bütün a elemanları için (a, a) oluşturulan bağıntının elemanı ise, bu bağıntıya “Yansıyan Bağıntı” denir.
∀ a ∈ A olmak üzere, (a, a) ∈ β ise, β yansıyan bir bağıntıdır.
Simetri Özelliği: Bir bağıntının her (a, b) elemanları için (b, a) ‘da bu bağıntının elemanı ise bu bağıntıya “Simetrik Bağıntı” denir.
∀ (a, b) ∈ β için (b, a) ∈ β ise, β simetrik bir bağıntıdır.
• β simetrik ise, β = β-1 ‘dir ve grafiği de y = x doğrusuna simetriktir.
Ters Simetri Özelliği: a ≠ b olmak üzere ∀ (a, b) ∈ β için (b, a) ∈ β ise, β bağıntısına “Ters Simetrik Bağıntı” denir.
• Bağıntıda (a, a) elemanının bulunması ters simetrik olma durumunu etkilemez.
Geçişme Özelliği: A bir küme ve β, A kümesinde tanımlı bir bağıntı olmak üzere; ∀[(a, b) ∈ β ve (b, c) ∈ β] için (a, c) ∈ β ise, bu bağıntı geçişme özelliğine sahiptir.
• A kümesi boş kümeden farklı ve A kümesinden tanımlanan β bağıntısı β = Ø bağıntısında yansıma özelliği bulunmaz. Geçişme, simetri ve ters simetri özellikleri bulunur.
Bağıntı Çeşitleri:
Denklik Bağıntısı: Tanımlanan herhangi bir bağıntıda yansıma, simetri ve geçişme özeliğini sağlıyorsa, bu bağıntıya “Denklik Bağıntısı” denir.
Sıralama Bağıntısı: Tanımlanan herhangi bir bağıntıda yansıma, ters simetri, geçişme özeliği varsa bu bağıntıya “Sıralama Bağıntısı” denir.
• β, A kümesinde tanımlı bir denklik bağıntısı olmak üzere (a, b) ∈ β ise a ve b elemanları β bağıntısına göre denktir denir ve “a≡ b” şeklinde gösterilir. A da a elemanına denk olan bütün elemanların kümesine “a’nın denklik sınıfı” denir ve ![]() şeklinde gösterilir. a’nın denklik sınıfının kümesi;
şeklinde gösterilir. a’nın denklik sınıfının kümesi;
![]()